Jaidon Smith

Hi! Thanks for stopping by. I’m Jaidon, computer scientist from Australia specialising in Artificial Intelligence and Statistics.

Note: The purpose of this post is as a personal reflection and not as a tutorial.

As part of building an automatic speech recognition tensorflow model I am researching and building transformers.

Some Useful Links

The Paper “Attention Is All You Need”

https://arxiv.org/abs/1706.03762

https://arxiv.org/pdf/1706.03762.pdf

TensorFlow

Tutorial: Transformer model for language understanding

Multi-head attention API

Position encoding

Tensor2Tensor

This was mentioned in the transformer paper as the original codebase.

“Tensor2Tensor, or T2T for short, is a library of deep learning models and datasets designed to make deep learning more accessible and accelerate ML research.”

It has since been replaced by Trax.

Automated Speech Recognition with the Transformer model

This was the only tutorial under the docs in github

Tensor2Tensor Transformer

Speech recognition transformer notebook

Inside transformer.py there are parameters for an automatic speech recognition transformer.

@registry.register_hparams
def transformer_librispeech_v1():
  """HParams for training ASR model on LibriSpeech V1."""
  hparams = transformer_base()

  hparams.num_heads = 4
  hparams.filter_size = 1024
  hparams.hidden_size = 256
  hparams.num_encoder_layers = 5
  hparams.num_decoder_layers = 3
  hparams.learning_rate = 0.15
  hparams.batch_size = 6000000

  librispeech.set_librispeech_length_hparams(hparams)
  return hparams


@registry.register_hparams
def transformer_librispeech_v2():
  """HParams for training ASR model on LibriSpeech V2."""
  hparams = transformer_base()
  
  hparams.num_heads = 2
  hparams.filter_size = 1536
  hparams.hidden_size = 384
  hparams.num_encoder_layers = 6
  hparams.num_decoder_layers = 4
  hparams.learning_rate = 0.15
  hparams.batch_size = 16

  hparams.max_length = 1240000
  hparams.max_input_seq_length = 1550
  hparams.max_target_seq_length = 350
  hparams.daisy_chain_variables = False
  hparams.ffn_layer = "conv_relu_conv"
  hparams.conv_first_kernel = 9
  hparams.weight_decay = 0
  hparams.layer_prepostprocess_dropout = 0.2
  hparams.relu_dropout = 0.2

  return hparams

Trax

https://github.com/google/trax

“Trax is an end-to-end library for deep learning that focuses on clear code and speed. It is actively used and maintained in the Google Brain team”.

Trax Documentation

Trax Transformer

TensorFlow Addons

Multi-head attention

Background: Attention

Tutorial on TensorFlow Site

A Blog post found by google searching “attention networks”

Seq2Seq: Motivated attention

Blog post linked by the other Buomsoo Kim post

Google AI Blog (Building Your Own Neural Machine Translation System in TensorFlow)

There is also a seq2seq google repository

TensorFlow Addon Seq2Seq Tutorial

Papers

https://github.com/tensorflow/nmt#background-on-the-attention-mechanism: “…attention mechanism, which was first introduced by Bahdanau et al., 2015, then later refined by Luong et al., 2015 and others”.

TensorFlow Tutorial

Following the tensorflow transformer tutorial

Positional Encoding

Normalisation

Scaled dot product attention

\[Attention(Q,K,V)=softmax_{k}(\frac{QK^{T}}{\sqrt{d}})V\]

It will be helpful to understand this formula in terms of the original attention formulas.

We first consider what \(QK^{T}\) means.

(The first dimension is the number of rows). For simplicity we ignore the batch dimension.

Q has shape (Sequence Length, d_dim) but must at least have shape (?, d_dim).

The first dimension is how many queries we want to make, this can go as high as Sequence Length which will give us the query for every position. However Q could also be dimension (1, d_dim) if we just wanted to compute 1 query like in the original attention paper. We will call the first dimension Q_dim.

This means that K must at least have shape (?, d_dim), where the first dimenstion is how many positions that we are are getting attention for. It is very natural to consider all of the positions giving K the shape (Sequence Length, d_dim).

and that \(QK^{T}\) has shape (Q_dim, Sequence Length)

For simplicity let us just do a query on one of the positions. We will call this q and it has dimensions (1, d_dim).

Comparing to the score in the original equation

In the original attention papers there were two main kinds of scores presented.

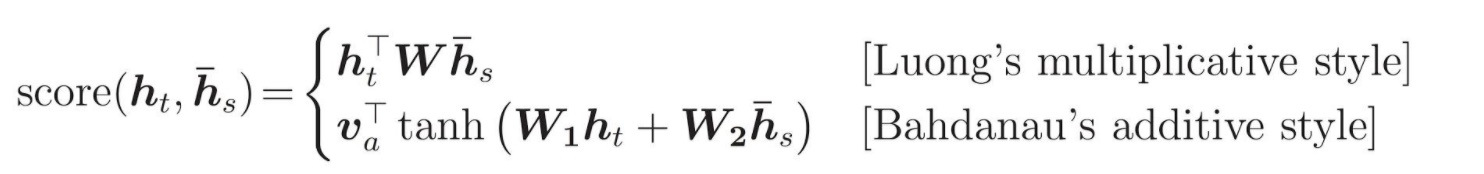
image1

It can be shown that \(QK^{T}\) part is equivalent to Luong’s score also called the dot-product attention. We need to note that the Q, K and V are not the direct h’s but actaully those with a matrix multiplication applied.

image2

The above image is from the paper but I will write the Q, K and V’s here as \(Q^{*}\), \(K^{*}\) and \(V^{*}\) in order to properly distinguish from the earlier notation.

By writing the product like this: \(Q^{*}W_{i}^Q(W_{i}^K)^{T}(K^{*})^{T}\), we can see how it could be comparable to Luong’s score.

Masking

The first thing to note is that in the tensorflow implementation, 0 means ‘can learn from’ or ‘consider’ and 1 means ‘prevented from learning from’ or ‘ignore’.

def create_padding_mask(seq):
  seq = tf.cast(tf.math.equal(seq, 0), tf.float32)
  
  # add extra dimensions to add the padding
  # to the attention logits.
  return seq[:, tf.newaxis, tf.newaxis, :]  # (batch_size, 1, 1, seq_len)
  
def create_look_ahead_mask(size):
  mask = 1 - tf.linalg.band_part(tf.ones((size, size)), -1, 0)
  return mask  # (seq_len, seq_len)
  
def create_masks(inp, tar):
  # Encoder padding mask
  enc_padding_mask = create_padding_mask(inp)
  
  # Used in the 2nd attention block in the decoder.
  # This padding mask is used to mask the encoder outputs.
  dec_padding_mask = create_padding_mask(inp)
  
  # Used in the 1st attention block in the decoder.
  # It is used to pad and mask future tokens in the input received by 
  # the decoder.
  look_ahead_mask = create_look_ahead_mask(tf.shape(tar)[1])
  dec_target_padding_mask = create_padding_mask(tar)
  combined_mask = tf.maximum(dec_target_padding_mask, look_ahead_mask)
  
  return enc_padding_mask, combined_mask, dec_padding_mask

target input was split into two kinds tar_inp and tar_real, it is tar_inp that is the target the mask is formed on in this way:

...

@tf.function(input_signature=train_step_signature)
def train_step(inp, tar):
  tar_inp = tar[:, :-1]
  tar_real = tar[:, 1:]
  
  enc_padding_mask, combined_mask, dec_padding_mask = create_masks(inp, tar_inp)
  
...

It is also tar_inp that is given to the decoder.

But it is tar_real that the loss is calculated on and thus what the output of the decoder is trying to predict.

Understanding the lookahead mask

mask = 1 - tf.linalg.band_part(tf.ones((size, size)), -1, 0)

From the band_part documentation:

Useful special cases:

tf.matrix_band_part(input, 0, -1) ==> Upper triangular part.

tf.matrix_band_part(input, -1, 0) ==> Lower triangular part.

tf.matrix_band_part(input, 0, 0) ==> Diagonal.

This means that

tf.linalg.band_part(tf.ones((size, size)), -1, 0)

is a (Sequence Length - 1, Sequence Length - 1) lower triangular matrix of ones and that:

1 - tf.linalg.band_part(tf.ones((size, size)), -1, 0)

Would be an upper triangular matrix of ones except that the diagonals are also all 0.

If we consider the ith row represents what outputs the ith position is allowed to learn from (rember the shifted outputs so the ith position is predicting i+1):

  • Position 0 can only use output 0 to predict position 1
  • Position 1 can only use outputs 0,1 to predict position 2
  • Position i can use outputs 0 to i to predict i+1